User:Eirisu
From Robin
eirisu@ifi.uio.no
Contents |
Master's Thesis:
- Stereo Vision and for Unmanned Ground Vehicle
My Master's Thesis concerns the use of optical sensors, in order to construct 3D-models of the area around an autonomous vehicle.
Timeline
October
- Finish Road-Detection Algorithm
- Implement the algorithm in C++ (Maybe as a ROS-node)
- Demonstration of the working system at FFI (October 30)
- Test 1
November
- Developement of the dirt-road version of the algorithm.
- Are the same approaches working in this terrain?
- Test 2
December
- Developement of map-representation (free-space, road, path, obstacle, etc.)
- Second test December 16.
- Testing of accuracy and speed.
- Classification
January
- Further testing of accuracy
- Start serious writing
Febuary
- Master's Thesis writing
March
- Deliver 1st draft for review
April
- Deliver 2nd draft for review
May
- Deliver Master's Thesis
Road Detection
One of the first things they want to achieve the Norwegian Defence Research Establishment (FFI), is an autonomous vehicle able to drive by itself at tarmac roads. Thus, I've begun making an algorithm that can detect where the road is in a color-image.
As a first step, I've chosen to take a segment of the image, and calculate the gaussian model for this section. The assumption is that the road is always right in front of the vehicle. Then, a region-growing search is executed to find the other 8-connected pixels belonging to the gaussian model, according to the Bayesian cost function:
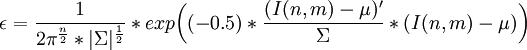
Bayesian Classification on RGB space
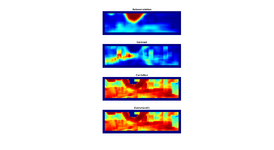
The results below is computed using only the RGB Color-Space as features and the bayesian cost function on a 373*113pixel image. The left images shows some good result. In these examples, the road texture is pretty homogeneous, and there is little ambiguity. The two images on the right shows some bad result. In the top image, the section right in front of the car, which is used for making a gaussian model for the road, is dominated by shadows, which causses the gaussian model to be false. Shadows are a problem, but there are methods to handle them. The bottom image shows a situation where there are several areas that displays simmilar RGB values as the road.
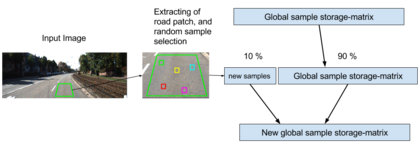
Improvement by Forwarding Samples
To make this naive frame-by-frame classifier a little more robust to sudden changes, an effective and simple approach is to forward samples from one image to another. For each frame, a set of road samples are extracted from an area in the image corresponding to what is right in front of the vehicle. Then, a random 10% of these samples are selected and appended to a random 90% of the existing road samples. The 10-90 ratio is just an example, and could be adjusted. The ratio is a trade-off between adaptability and robustness to sudden change.
Texture-Based Approach
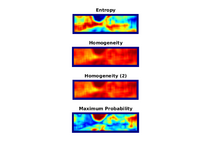
I've experimented with using the Gray-Level Co-Occurence Matrix (GLCM) in order to extract textural information from the image. In my experiment, I've computed the GLCM for a 31x31pixel window surrounding each pixel in the image. Then, 26 different features are computed by applying different functions on the GLCM. I've tested different combinations of these features, to see what feature-combination provides the most robust differentiation. Below are some of the best features I found:
Optimization using Expectation Maximization
Road images often contain different elements which makes classification difficult. Difference in lighting, shadows, texture variance etc. contributes to making the class distribution of road complex. Until now I've tried to find features which are robust to these differences, but another approach is to make the model, which represents the road class, more sophisticated. To make the gaussian model of to the road features more complex, I've utilized the Expectation Maximization algorithm. The algorithm is originally a clustering algorithm, which tries to fit K gaussian models to a feature space. However, instead of using the models as clusters, I use it as a distance meassure. By estimating the probability density function across all the models, we can achieve a distance meassure that takes into account a complex class spread:
- We construct K gaussian models, each with its own mean μi, and covariance matrix Σi.
- We then weigh each of these models with a factor ωi, based on the number of samples belonging to each.
- We then compute the probability density function across all the gaussian models:
where fpdf(x | μi,Σi) is given by:
where D is the number of features in the feature-space.
Below are an example of a single run of the algorithm.
However, we can further develop this method by letting these gaussian models develop over time (i.e. from image to image):
- The first image captured leads to the first K gaussian models.
- For each image captured after that we make K new gaussian models.
- We compare each old model to each new by the Mahalanobis-distance between the models.
- If the distance is sufficiently low, the current gaussian model is updated by a factor of the new gaussian model's properties.
- If not, the new model takes over for the weakest old gaussian model in the existing gaussian-mixture-model.
Below are an example of the algorithm applied on some image sequences from the KITTI-dataset.
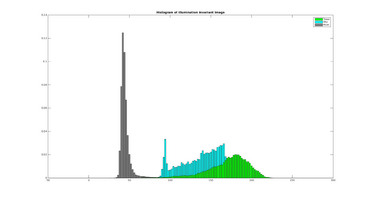
Illumination-Invariant Images
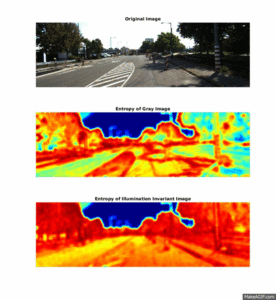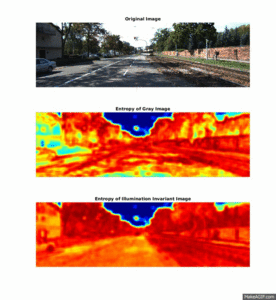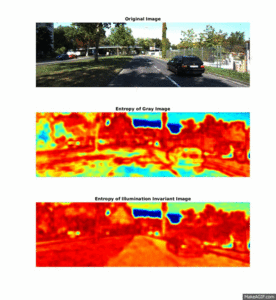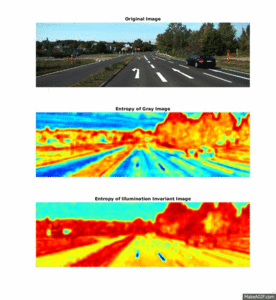
Shadows and different lighting conditions are a big problem for many segmentation algorithms. Therefore, it is beneficial to be able to filter out these differences in lighting, before segmentation is initiated.
By using knowledge about the camera's spectral response, one can compute an illumination-invariant picture by the following formula: ii_image = 0.5 + log(IG) − α * log(IB) − (1 − α) * log(IR), where α is the spectral response coefficient for the particular camera, IR,IG,IB represent the original image seperated into the three RGB color channels, and ii_$image is the illumination-invariant output image.
Results
II-Image for Improving Textural Feature-Images
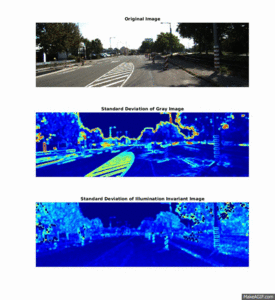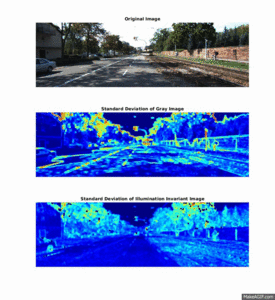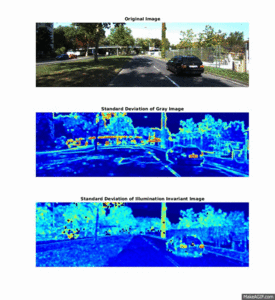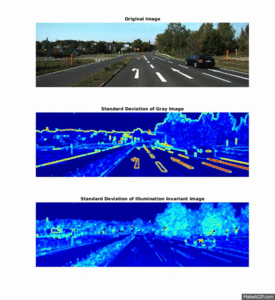
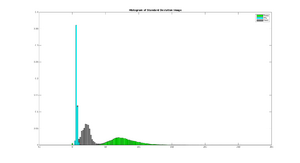
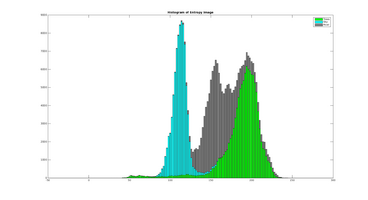
This section illustrates how textural feature-images computed from the illumination invariant images are more robust to noise in the road, and produce a higher seperation between the different elements in the scene.
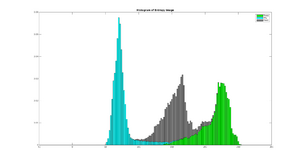
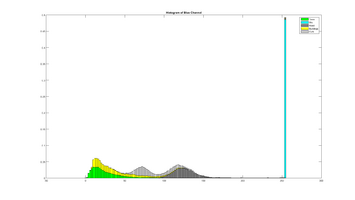
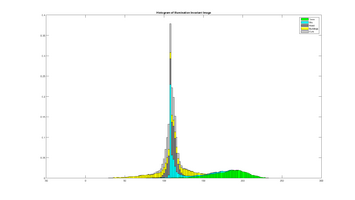
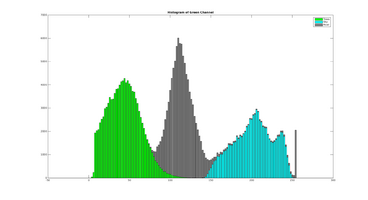
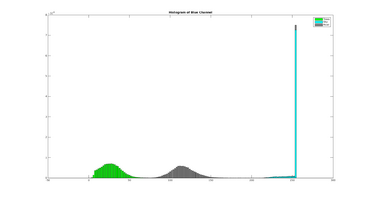
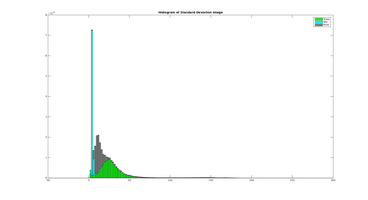
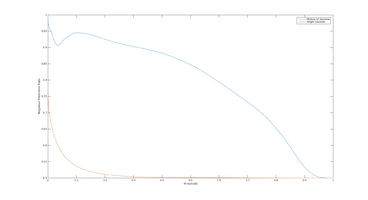
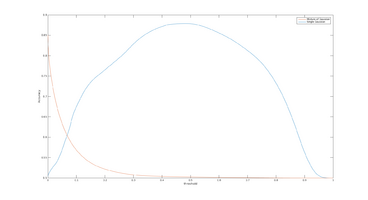
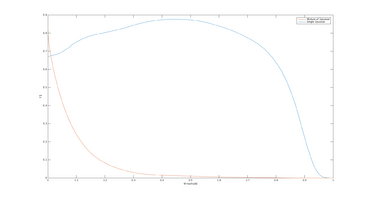
The two plots below shows the histogram of the Entropy image and Standard Deviation image, calculated from the three scenery objects "Road", "Sky" and "Trees, and illustrates how the different objects are more seperated than in the results: Entropy um_000067, Standard Deviation.
Vanishing Point and Road Edge Detection
Vanishing Point Detection
A vanishing point is a point in the image where parallel lines seems to meet, from the observer's perspective. Vaninishing points have a lot of applications in computer vision (camera calibration, SLAM, 3D reconstruction), but for road detection it can help refine the search space. Since the vanishing point is a point far away from the observer, and since our application is always stationed on the ground, we assume that pixels above this point is either too far away, or nearby obstacles.
To detect these vanishing points, I've used an edge-detection filter, known as Gabor filter, defined as a 2D sinusoid multiplied by gaussian. The phase of the sinusoid determines the orientation of the Gabor kernel, and by convolving the image with a Gabor kernel of a specific orientation, we get a probability of each pixel belonging to that orientation. The purpose of using this technique is to find an individual orientation probability for each pixel. I therefore construct multiple Gabor kernels with different orientation. It is also a good idea to construct Gabor kernels of different scales, to be able to detect lines of different thickness.
I've constructed a Gabor filter bank at 8 different orientation between 0 and 157.5 degrees, at 5 different scales. To get a probability estimation of the pixel orientations, I've done the following:
- Convolve the image with each of the Gabor kernels Gω,φ to get 8x5 bank of filtered images.
- For each filtered image, compute the complex response: Iω,φ(x,y) = Re(Gω,φ(x,y))2 + Im(Gω,φ(x,y))2
- For each pixel in the complex response images, compute the average of the 5 scales: Rφ(x,y) = meanω(Iω,φ(x,y))
- Then finally, the pixel orientation of each pixel is estimated by finding the maximum of each pixel the 8 response images: θ(x,y) = ArgmaxφRφ(x,y)
At the last step, in order to avoid too much noisy classification, we introduce a confidence threshold for the orientation estimation. This involves only estimating an orientation if the detected maximum orientation, compared to the other orientations, are above a certain threshold.
From this, the vanishing point is estimated by a voting scheme. We iterate through the orientation image θ, and for each pixel we do the following:
- Find all pixels below the current pixel P, within the radius r = 0.3 * imageHeight.
- For each sub-pixel V:
- We calculate the angular difference γ between the orientation of V, and the angle between the V and P, is lower than a certain threshold, P is voted for.
- The voting-score is a function of this angular difference, and the distance, d(P,V), between the two pixels:
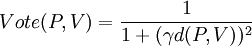
- The pixel which receives the highest score, is determined as the vanishing point.
Below is a visualization of the different steps of the algorithm.
Road Edge Detection
When a vanishing point is detected, the road edges can be estimated. The algorithm is quite straight forward:
- First apply an edge-detector on the input image, for instance Canny.
- Detect the strongest N strongest edges through Hough-transform.
- Filter out edges that are close to horizontal and above the vanishing point.
- Sort the N strongest edges into left edges and right edges, depending on weither their midpoint is on the left or right half of the image.
- For each line in each of these two sets:
- Extract k sample-points (pixels) on the line.
- For each point, calculate the angular difference between the pixels orientation and the lines orientation.
- If the angular difference is below threshold, the line receives a vote.
- Extract two patches on either side of the line, A1 and A2.
- Compute the difference between these two patches:
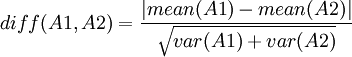
- Compute the difference between these two patches:
- The lines score is multiplied with the difference between A1 and A2.
- Extract k sample-points (pixels) on the line.
- When the highest scoring left edge and right edge is found, we refine our search space as the area going from the vanishing point, through the lowest point on each of the edges, to the image boarder.
Below are some result from the algorith:
Feature Analysis
This section contains an analysis over how well the different features seperates basic objects in a typical road scene (road, trees, buildings, sky, etc.).
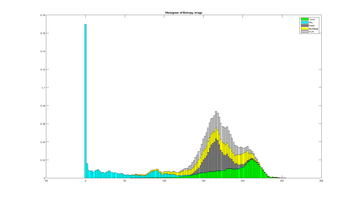
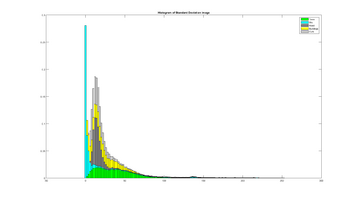
To distinguish between different objects, I have manually labeled some test images (like the one above). The different objects are seperated into individual 6-dimensional features images, which is then again reshaped into a 6 * Si matrix, where Si is the number of samples (pixels) belonging to that object, and 6 is (currently) the number of features used. Then, for each the 6 features, the histograms of the different objects are computed, which allows visual analyzation of the objects spatial distribution with respect to the current feature space.
Example
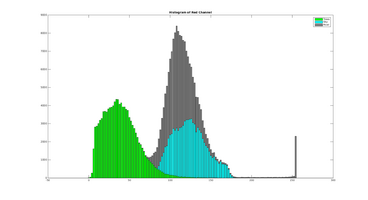
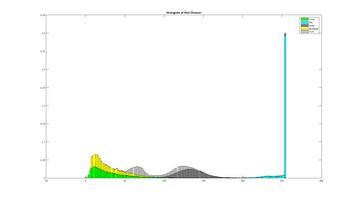
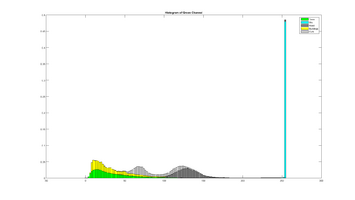
This subsection contains an example using the red color chanel. Below is the original image, and 3 labels for road, sky and trees.
The image is then split into 3 individual images:
These serves as our samples for computing the histogram. The histograms are computed using 100 bins
Results
KITTI - um_000001
KITTI - um_000067
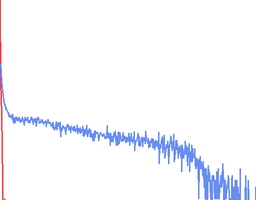
Speeding Up Entropy Computation
The computation of the Entropy feature-images is by far the heaviest. The method involves computing the histogram of a local window, and the using the histogram-counts to give a meassure of 'disorder'. This meassure is given by the equation E = − Σp * log2(p), where p is the histogram counts.
The regular method for doing this, is to have a sliding window from which the histogram is computed. The problem with this method is that a sliding window iterates over the same values multiple times (depending on the window size), even though the inpact on these values on the histogram does not change. So, to avoid this extensive computation, we instead just concider those rows and columns that appears/disappears from the "window", and simply increase/decrease the histogram-count at the histogram-index equivalent to these gray-level values. The number of operations performed at each is decreased from N2 to 2N.
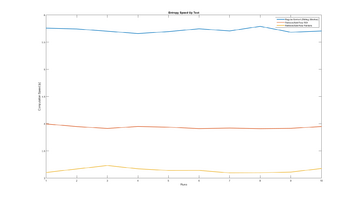
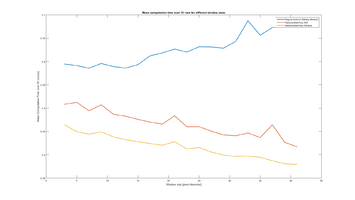
Evaluating road-estimation algorithm
There are several parameters that affects the estimation quality of the algorithm. In these tests I whish to statistically determine the effect to the following:
- Window sizes for computation of Entropy- and Standard Deviation-Image
- Effect of blurring II-Image at different window sizes.
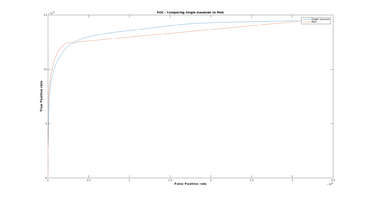
- Difference between Single Gaussian distribution and MoG distribution
- Effects of different resolution on input-image
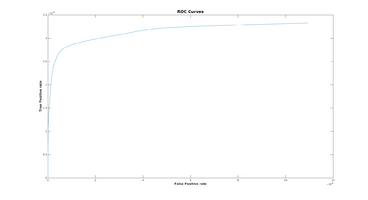
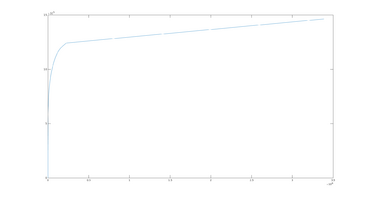
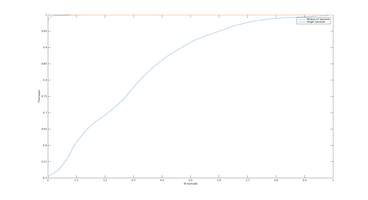
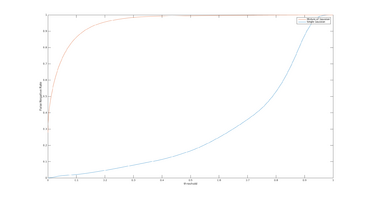
ROC Curves
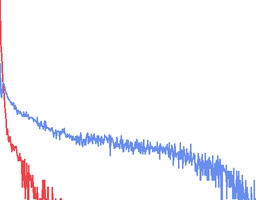
In order estimate how well the estimation algorithms performs across different runs (with different parameters), I've chosen to use "Receiver operating characteristics", or ROC Curves. ROC Curves displays the releationship between "True Positive Rate" and "False Positive Rate" at different thresholds.
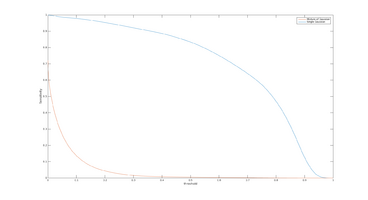
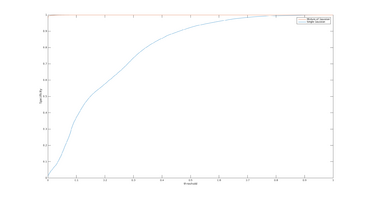
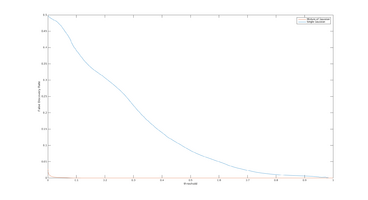
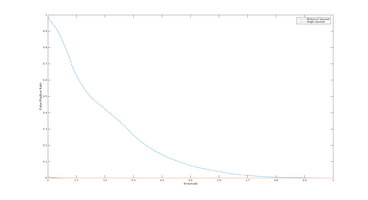
Other Statistical Measures
Below are some other statistical measures that could be appropriate to use in the evaluation of the road-estimation algorithm. All measures are computed using True Positive Rate (TP), False Positive Rate (FP), True Negative Rate (TN) and False Negative Rate (FN).